各个空间与对应的变换
每个3D模型都有自己的局部空间(Local Space)。空间拥有自己的局部坐标系,定义了自己的原点位置。
经过模型变换(Model Transformation)后,应用model矩阵变为世界空间(World Space)。具体的变换过程取决于我们想把模型放在世界的哪个位置。
经过观察变换(View Transformation)后,应用view矩阵变为视图空间(View Space)。主要为了实现视角变换(摄像机位置的改变)
经过投影(Projection)后,应用projection矩阵变为裁剪空间(Clip Space)。这一步将视锥进行线性变换,裁剪视锥外的区域,存储压缩信息,便于后续变换到NDC。
经过齐次除法后,变为NDC(Normalized Device Coordinates)。这一步变换到一个范围为[-1,1]的正方体中。
经过视口变换(Viewport Transformation)后,变为屏幕空间(Screen Space)。将NDC坐标映射到[0, 屏幕宽度] 和 [0, 屏幕高度]。
World Space与View Space
这两个空间的区别仅在于摄像机位置不同,导致两个坐标系不同。在GAMES101的作业3中大量使用了View Space坐标来计算各种插值、Blinn-Phong模型等,这是因为作业3中固定了摄像机视角,View Space坐标更方便。
而在视角可能变化的情况中,上述计算更多会使用世界坐标。
在作业3的draw函数中:
//仅应用view和model矩阵,因此mm中是view space下的坐标
std::array<Eigen::Vector4f, 3> mm {
(view * model * t->v[0]),
(view * model * t->v[1]),
(view * model * t->v[2])
};
std::array<Eigen::Vector3f, 3> viewspace_pos;
//截断得到三维的view space顶点坐标
std::transform(mm.begin(), mm.end(), viewspace_pos.begin(), [](auto& v) {
return v.template head<3>();
});
//传入光栅化
rasterize_triangle(newtri, viewspace_pos);截取的这一段展示了draw()如何得到View Space坐标。如果仅应用model矩阵,就可以得到World Space坐标。
由于光照计算需要模拟三维空间的物理规律,插值计算也需要符合三维下的几何特征,这些计算都需要用这两个坐标中的一个进行。
Clip Space(透视投影矩阵)
先看这个视频https://www.bilibili.com/video/BV1LS4y1b7xZ
看完后就知道透视投影矩阵是怎么来的了,以及能够知道齐次除法如何通过矩阵实现,w为什么是view space中的-z。这个推导过程不难
【这里等待补充文字讲解】
经过透视投影矩阵变换后,空间就变为了clip space:
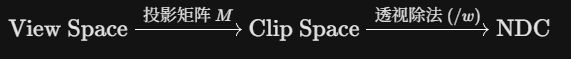
这样就会得到w=-z的clip space坐标,等待进行透视除法。这一步需要保存下来,因为我们还需要view space中的z值来帮助我们插值,转换到NDC之后就丢失这个信息了。
透视投影还有个非常重要的点:投影后,远近平面会反过来。透视除法后,近平面会被映射到NDC的-1,远平面被映射到NDC的1。也就是说,标准右手系中,投影前是z越小越远,投影后是z越小越近(这里的z是投影后的z,不是view space中的z)
这一点在上面的视频中有动画演示,因此深度测试需要找出z更小的像素渲染,来反转这个关系。
NDC和Screen Space
经过齐次除法后,变换结果被限制在 {[-1,1]}^{3} 的范围内,这个结果就是NDC。
再将NDC映射到屏幕的长宽上(简单的缩放,对每个本来在[-1,1]中的点乘一下缩放系数就行),即可得到Screen Space。
【重要】rasterize_triangle实现
这个函数用于光栅化单个三角形,它在draw()中被调用。尽管不同作业中的draw()实现方式不一样,但都是通过某种方式传入了一堆三角形,进行一些预处理(作业3分析)后逐个调用rasterize_triangle()进行光栅化。
它的实现大致步骤如下:
计算获取三角形的bouding box,遍历其中的每个像素,获取每个像素的中心坐标(+0.5),据此判断是否位于三角形内部。
若不在三角形内部,则跳过该像素;若在内部,则通过后续步骤光栅化。
通过重心坐标,插值计算该像素的z-buffer近似值。

