这节课虽然内容相对比较浅,但是总量特别多,全部搞懂还是比较累的。
这节课内容涵盖了Blinn-Phong reflectance model的完整形式以及核心思想,着色频率,渲染管线等,下面逐个分析。
Blinn-Phong reflectance model
Blinn-Phong模型将每个着色点的反射强度计算分为三个部分:漫反射(Diffuse),镜面反射(Specular)和环境光(Ambient)。
尤其注意,Blinn-Phong模型实际上是个经验模型,是通过数学方法模拟现实中的物理行为,因此我们应该抱着"这个模型能不能模拟出现实里的规律"的态度对待它。
请注意,下面所涉及到的向量,若无特殊说明皆为单位向量。
漫反射(Diffuse)
如下图,漫反射项 L_d的计算旨在模拟以下几个因素:
漫反射系数 k_d:通常是一个RGB向量,表示当前材质在不同颜色通道下反射光线的能力。取决于材质本身的性质(最重要)、表面粗糙度等等,比如金属的 k_d通常较小,粗糙的表面 k_d通常较大。但这并不意味着k_d 能决定渲染出来的质感,实际上对质感影响最大的仍然是材质贴图。
光线能量衰减 \frac{I}{r^2}:光照以球形向外发散衰减,数学上可以认为其与表面积成正比,因此除去常数后的形式就是 \frac{I}{r^2}。
角度对能量接收的影响 max(0,n \cdot l):反射出去的能量比例。这是个很直观的结果,表示入射光与法线夹角越小,能量越大。
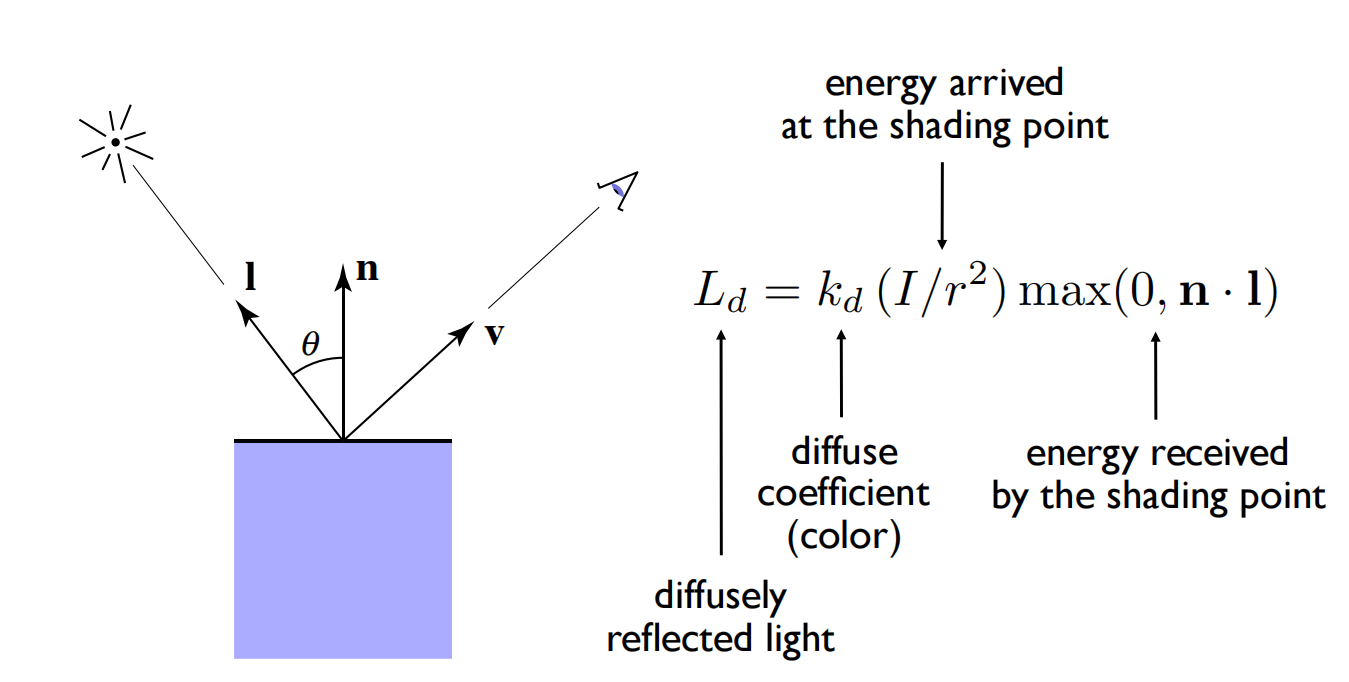
漫反射是非常均匀的,在任何方向上观察的结果应该都是一样的。因此图中的观察向量v只是一个示例,对结果没任何影响
上面对公式中的各个项做了解释,可以发现它们非常不严谨,这样真的效果会好吗?事实上这种形式的Blinn-Phong模型确实不太精确,但它仍然可以很大程度地模拟出现实反射的效果。
在电脑中渲染一张图片,我们需要的是正确的视觉效果,而不是与真实世界一模一样的物理规律。因此,我们的重点在于哪些因素会影响反射的强度,以及如何模拟它。
光线能量衰减项 \frac{I}{r^2},显然真实世界中绝对没有这么简单,这个公式理论上是这样推导的:
也就是说,最核心的部分是 I_d \propto \frac{I}{ r^2},只要实现这部分,光照衰减的速度就合理了,分母中的常数并不影响模拟。如果模拟的效果不理想,我们可以统一为所有材质的 k_d做修正,让它负责弥补省略常数所带来的误差。k_d 还能容纳很多这样的修正,因为这种误差对所有材质都是同等的。
但虽然k_d 承载了"修正"的任务,它本身的物理含义仍然是最重要的:漫反射的反射程度:

镜面反射(Specular)
镜面反射项就更工程了,因为镜面反射在真实世界中的规律更复杂:
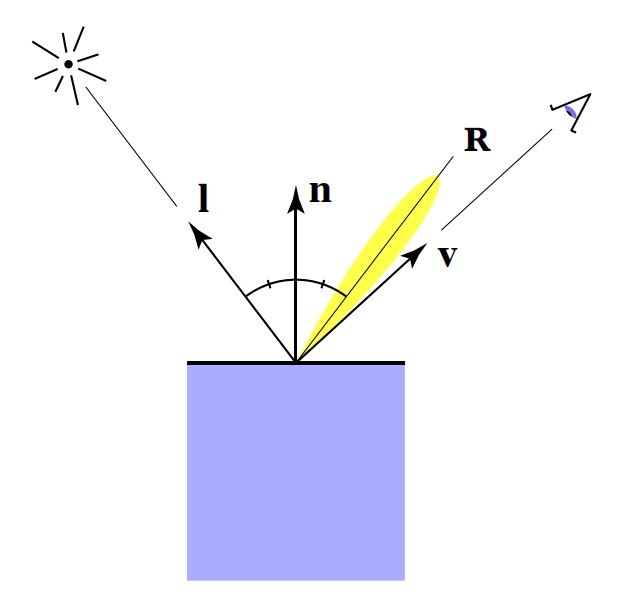
镜面反射和漫反射的形式很像,它们最大的不同是对角度的处理方法不同。
镜面反射在视觉上几乎全部以高光的形式体现,因此镜面反射只需要处理好高光即可。而高光是一个非常集中、与观察方向高度相关的视觉效果。入射角度对高光的影响非常小。具体而言:
就算是非常倾斜的入射角度,只要观察方向与出射方向接近,高光仍然会非常亮
就算是近乎直射的入射光,如果观察方向偏离太多,仍然无法看到明显的高光。
所以在Blinn-Phong模型中直接省略了入射角度对镜面反射的影响,我们只需专心处理好最重要的观察角度v。
如何衡量观察角度的影响?
再次强调,Blinn-Phong模型是一种经验模型,我们的目标是模拟出现实世界的效果。现实中,如果观察方向与出射方向重合,此时显然是高光最明显的位置;当观察方向偏离出射角度,高光自然就会变淡。因此我们得出第一个简单的规律:观察方向v与出射方向R的夹角越大,镜面反射越弱。
自然而然我们想到了通过余弦函数模拟这个效果: max(0,v \cdot R) ,这就是最初的Phong模型所采用的方式。
而Blinn-Phong模型在这个基础上做了计算上的优化。Phong模型中的计算方式需要先得出出射方向 R ,这个计算量非常大,公式如下:
这个计算太复杂了,于是Blinn-Phong模型尝试通过半程向量h(l与v的角平分线方向)与法线方向n的夹角来替代R与v的夹角,即通过 max(0,n \cdot h) 来模拟。经过计算,n与h的夹角是l与v夹角的两倍,可以完美替代!(因为它们是完全线性的关系,数值上的差异可以修正)
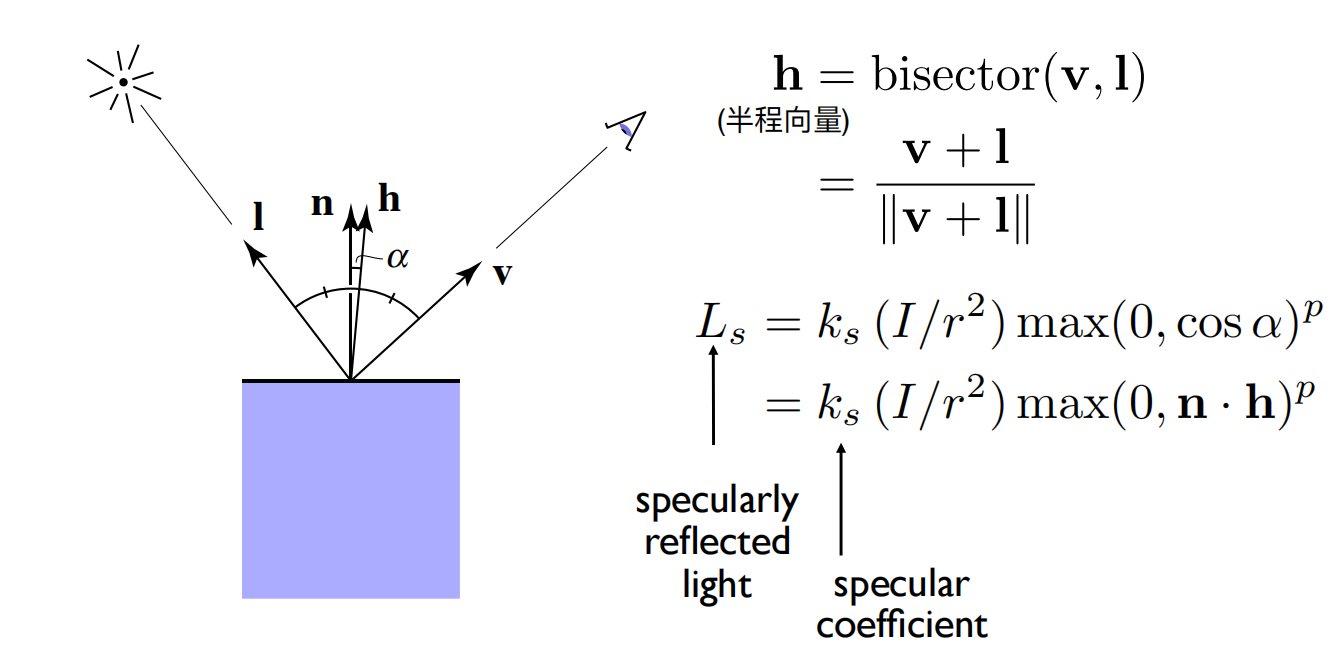
但为什么h与n的夹角更好算呢?h是角平分线,它可以通过v+l快速确定方向,然后正则化即可。显然这比计算出射方向R要简单的多。
曾经我有这样的疑问:n不就是l与R的角平分线方向吗?那不就可以用l+R来确定n的方向?反过来,不就可以用l-n来确定R的方向吗?
这句话前半句是对的,确实可以用l+R来确定n的方向,但反过来就不对了,l-n并不是R的方向。我们假设l+R的结果是N,N与n同向,但模长不同。我们只知道n是单位向量,但不知道N具体是多长。所以我们只能确定l-N是R的方向,无法确定l-n是不是R的方向(显然绝大多数情况都不是)
观察角度的影响不是线性的
对于漫反射而言,我们只需要大概模拟出角度越大,反射能量越弱的规律,直接套一个cos上去就能近似了。
但镜面反射不一样:现实生活中,观察角度有一点点小偏差,似乎对高光(镜面反射的表现)的影响不大;但若观察角度偏差到了一定阈值,继续偏差下去,高光就会急剧衰减。
为了模拟这样的规律,我们考虑为max(0,n \cdot h) 加一个指数p,p越大,余弦函数就越陡峭:
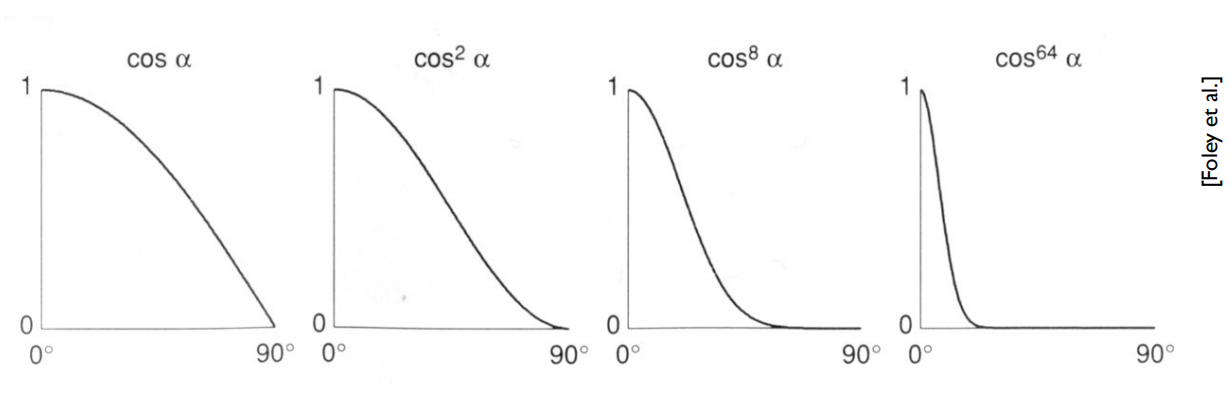
一般来说,p的取值在150甚至200左右才能比较好地模拟出现实高光的效果。此处可以利用快速幂进行大规模的指数运算。
下面有一个镜面反射公式中ks与p对高光影响的直观图示:

可以看到,p越大时,高光越集中
环境光(Ambient)
环境光项是最简单的一部分,它是用来解释物体在没有直接光照的情况下,为什么还能被看见。
环境光是一种不依赖于任何因素的基础着色,几乎相当于给整个空间提亮一个常数的亮度,公式如下:
它几乎完全由环境光反射系数 k_a 和环境光强度 I_a 决定。
现实世界中,即使光线没有直接照射在物体表面,光线也会透过墙壁、地板,或者以其他物体的漫反射的形式到达物体。因此大部分情况我们是无法在现实世界观察到"绝对的死黑"的。因此需要一个环境光来填充这些"死黑",模拟现实世界。
显然这只是一个简单的替代方案,用来模拟现实世界中各种杂七杂八的光线。这里的模拟方法就是整体提亮,因此成了blinn-phong模型中最简单的一项,但代价就是模拟效果并不完美
为了完美计算真实世界的环境光,我们需要尽可能多地计算所有能考虑到的光线的反弹,尽可能多地考虑反弹次数,以及各个物体对这些杂质光线的阻挡。这就是全局光照,或者说光线追踪,是目前图形学最复杂计算量最大的问题之一。
最后,Blinn-Phong光照模型可以总结为下图:

着色频率(Shading Frequencies)
先看下面三个从同一个球体模型(意味着面数量一样)渲染结果:

很显然它们的效果是从左到右越来越好的,同样的模型为什么会有这样的差异?答案是它们的着色频率不同。
我们有三种着色频率/方式,它们都围绕法向量展开,如果着色点确定了,那法向量就几乎决定了着色结果。
可以想象一下,如果一个三角形只有一个法向量,那这个三角形渲染出来一定只是个平面。但一个三角形有一百个法向量,如果这一百个法向量都能正确表达模型真实的情况,那这个三角形就会变的无比光滑!
Flat Shading
Flat Shading着色是以三角面为单位的,一个三角面只有一个法向量,根据这个法向量进行着色。这个法向量也很好计算,随便挑两条边叉乘一下就行了。
着色点的选取取决于渲染管线怎么实现的,比如有用三角形中心、重心的,也有直接用一个顶点的
这种着色方式对光滑的模型来说效果很差
Gouraud Shading
Gouraud Shading更进一步,首先让三角形的三个顶点都有各自的法向量(后面讲如何计算),对每个顶点先进行一次着色。然后用这三个定点的颜色对三角形内部的像素进行颜色插值。同样的模型中效果比Flat Shading好很多。一个三角形算三次光照,计算量也比Phong Shading好太多了。
但它有个致命的缺点:"消失的高光"。
"消失的高光":如果高光正好打在了三角形内部,离三个顶点都比较远。根据前面的分析我们知道高光如果偏移达到阈值,高光强度会猛降。此时本应有高光的像素完全不知道自己有高光,而是从三个感知不到高光的顶点插值了一个颜色,高光就这么消失了。
更糟糕的是,一个模型就只有那么几处有高光,一旦高光被吞掉一个,对整个模型的影响非常明显。
因此现代图形学基本不用Gouraud Shading了。
Phong Shading
Phong Shading的思想至今仍然被广泛应用,经久不衰。
现代的phong shading作为一种思想仍然盛行在图形学中(逐像素着色),只是具体实现方式变成了PBR(Physically Based Rendering)
Gouraud Shading是对三个顶点的颜色进行插值,而Phong Shading是对三个顶点的法向量进行插值。通过插值得到每个像素的法向量,再对每个像素进行着色(光线计算)。计算量非常大
如果一个三角形覆盖的像素很多,那phong shading一个面的着色很可能就需要百万级的计算(这对现代GPU也是小意思)。但现代图形学应用中都更倾向于制作更精细的模型,面数越来越多。精细的极限就是一个三角面只约等于一个像素
那精细到极限之后呢?flat shading和phong shading又有什么区别?这个问题曾经出现在图形学界过,答案是:在粗糙表面上没什么区别,但是在光滑曲面上还是有区别。因为即便精细到像素大小,flat shading还是按照平面微分的思路着色,但phong shading赋予了像素之间更平滑的过渡,更像曲面,也就是说,phong shading此时能一定程度弥补分辨率的不足!
并且精细到极限之后,计算才是最重要的问题。因为现代GPU是以quad(2x2像素块)为单位工作的,如果真的精细到像素级别,一个quad有四个三角形,性能上太差了。因此UE5 Nanite即使做到了像素级几何体,也不能直接用传统的管线去画,而是要发明一套全新的、基于 Compute Shader 的软光栅化管线
下面这张图展示了不同面的数量和不同着色频率对渲染效果的影响。
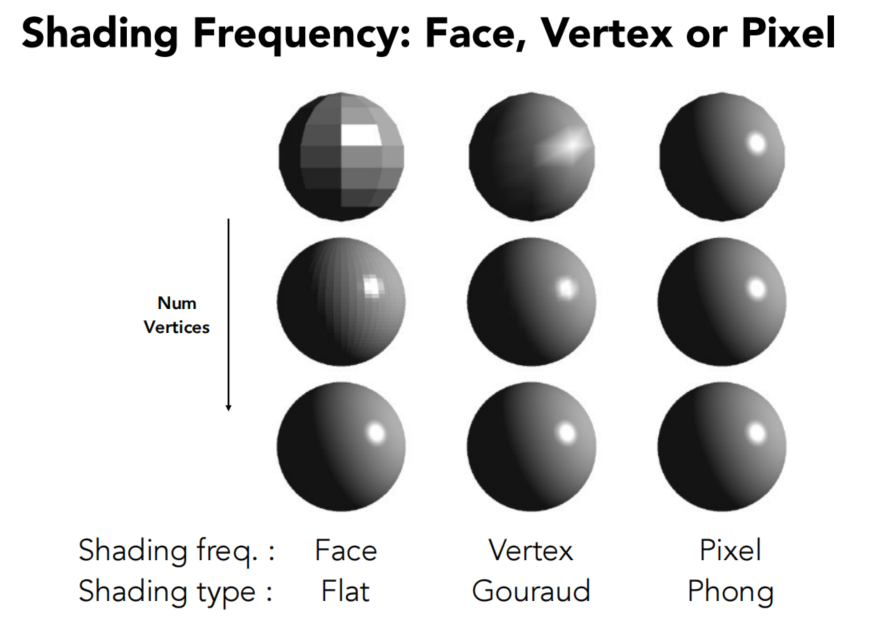
同样的面,高频率着色会更好;同样的频率,面数更多会更好
所以更高的着色频率实际上是在面不够多(模型不够精细)时的近似计算,多出来的信息都是插值出来的
如何计算顶点法线?
顶点法线有两种情况。
对于最理想的,模型形状已知的模型,我们可以直接取模型表面在该点的法线。但这太理想了,现实很难有这种情况
对于其他更复杂的模型,可以考虑将点所接触到的所有三角面的法线做平均:
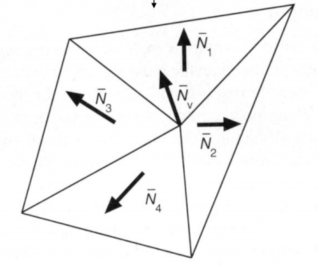
但这还有个问题:如果有些三角形太大,有些三角形很小,就会失真。于是我们可以按三角形面积进行加权平均。
即便是按面积加权平均,仍然不完美,因为法线最好的方向不一定是朝面积大的那一边偏的。于是后面又提出了按角度加权平均,这几乎是现代自动计算法线最主流的方式了。
上述方式所计算的法线是为了让模型更平滑,有些情况则需要更棱角分明,比如立方体的顶点,现代引擎会做断开平滑(Smoothing Groups / Hard Edges),一个立方体顶点实际上有多个点组成,有完全不同的法向量,使得模型的边角锐利。
现代图形学更多情况下已经完全不信任自动计算方法了,顶点法向量大部分时候都是靠美术任意自定义,写死在模型中,因此模型会自带法向量的,这事不用我们操心。

