点积与叉积在图形学的简单应用

点积(Dot Product)

高中我们都学过点积的几何定义（这里需注意\hat a 表示方向和\vec{a}相同的单位向量 ）：

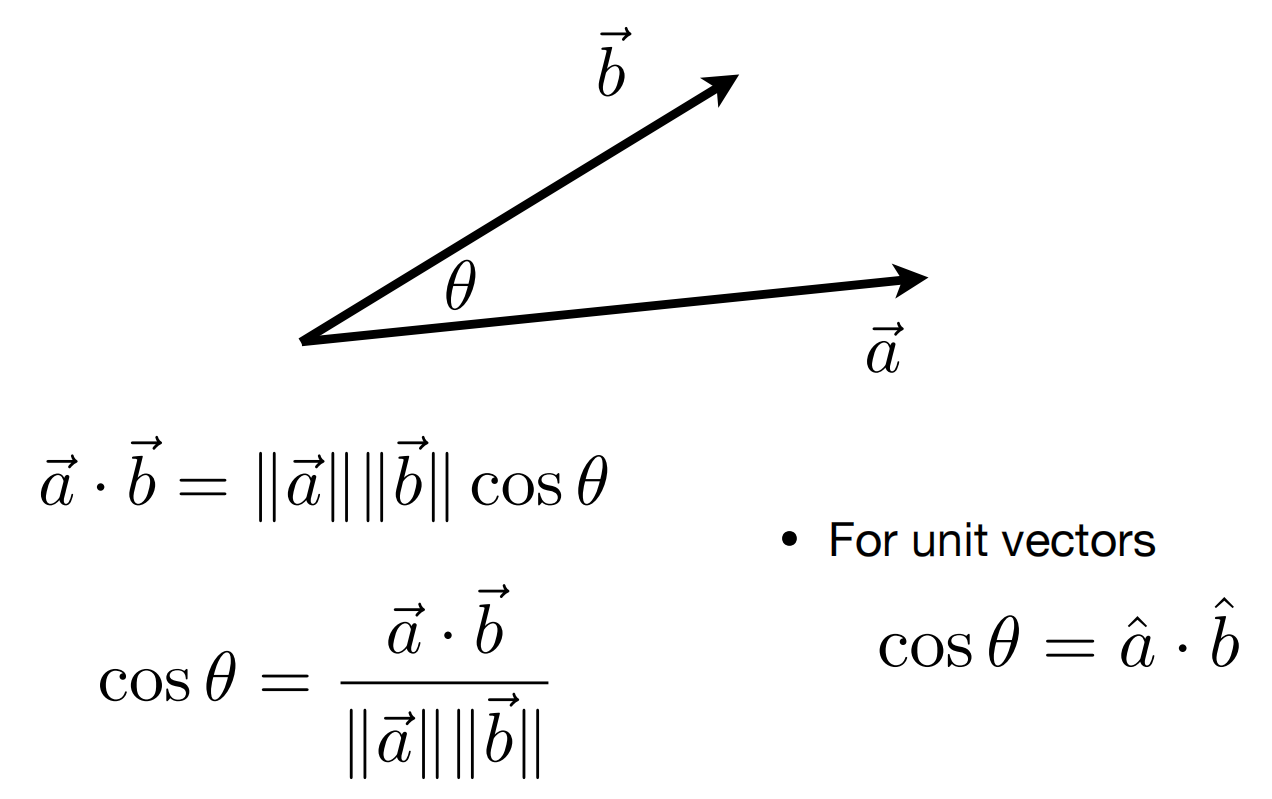
以及在坐标系中的代数定义 ：

注意，点积没有结合律，也就是说点积是只存在于两个向量之间的运算。不能随意结合


那么点积在图形学中有哪些具体应用呢？下面举几个最简单的例子来建立概念

  • 衡量两个向量方向有多接近： \vec{a} \cdot \vec{b}的结果越大，表示两个向量方向越接近

  • 计算两个向量的夹角

  • Projection：计算向量间的投影：

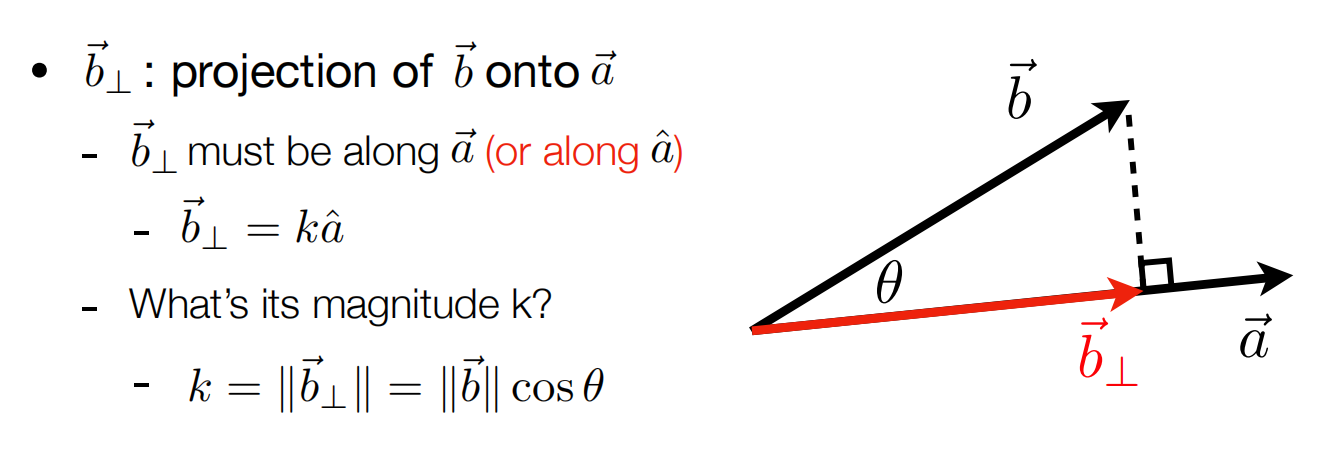
  • Decompose：在上述投影的基础上，分解一个向量为多个向量的和

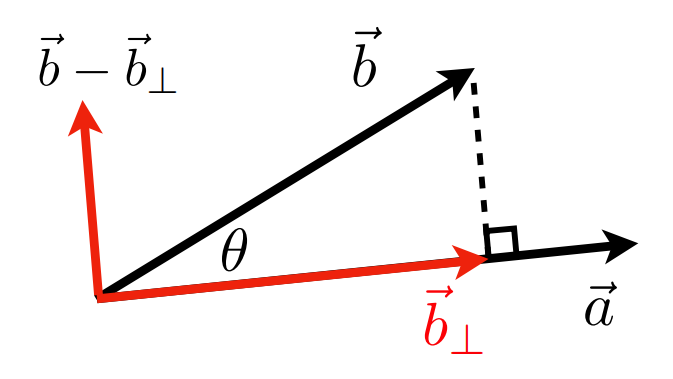
  • 通过点积判断两个向量是否"大体上"同向，假设通过 \vec{a}定义了“前方”，可以通过计算与\vec{a}的点积判断另一个向量是向前还是向后(forward or backward)

叉积(Cross Product)

简单复习叉积的基本概念：

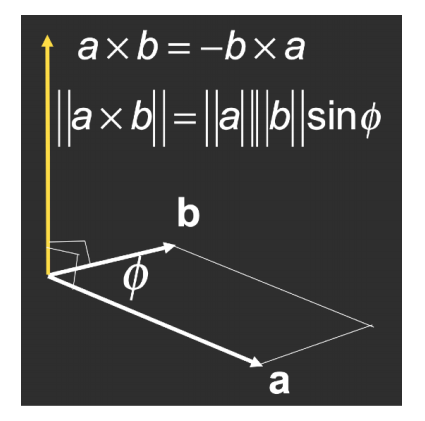
叉积的方向由右手定则决定，用右手比出点赞的手势，保证四根手指旋转的方向先经过 \vec{a}再经过 \vec{b}，拇指所指的方向就是叉积的方向

由此注意到两个很重要的性质：

  • 很显然叉积不满足交换律，右手定则中就强调了这一点

  • 叉积的方向是两个向量组成平面的法向量

尤其是上述第二点性质，在图形学中非常有用！

  • 判断向量是在"左边"还是"右边"：

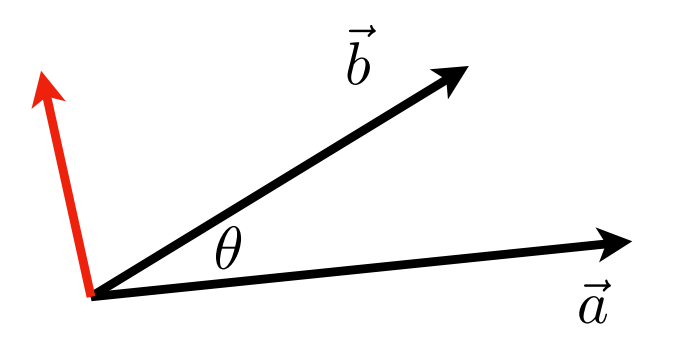    显然，如果 \vec{a} \times \vec{b}的结果为正向，则\vec{b}位于\vec{a}的左边

  • 由上面的结论进一步拓展，我们可以观察一个点是否位于某个多边形内部

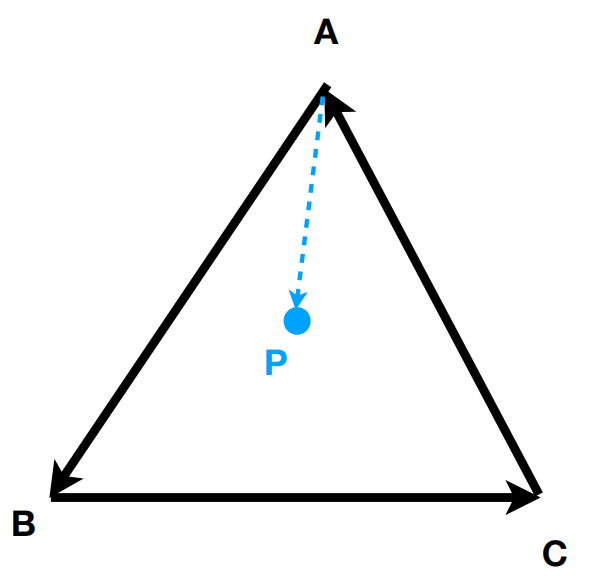    如果AP位于AB的左边，BP位于BC的左边，CA位于CP的左边，那么显然P一定位于三角形ABC的内部
    这里有个有意思的问题：如果这个三角形的方向从逆时针换成顺时针，上述结论不就失效了吗？
    于是进一步拓展：如果AB与AP的叉积，BC与BP的叉积，CA与CP的叉积，这三个结果同号，那么P位于三角形内部
    上述结论适用于任何多边形

  • 叉积还可以用于建立坐标系(Coordinate systems)，给定三维坐标系的两个轴，利用叉积可找到右手系的第三个轴