线性变换(Linear Transformation)的本质

线性变换主要是旋转和缩放，是一种"均匀"的变换。一定能被一个实矩阵表示

通过3b1b的线代基础视频：线性代数的本质 - 03 - 矩阵与线性变换，我们知道线代变换矩阵的一种本质理解：

\begin{bmatrix} x_{out} \\ y_{out} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x_{in} \\ y_{in} \end{bmatrix}

二维下的线性变换

其中 R= \begin{bmatrix} a & b \\ c & d \end{bmatrix} 是线性变换矩阵。一般来说，想要将目标变换的线性变换矩阵写出来，只需要看这个变换中坐标轴变换后的结果，组合即可得到线性变换矩阵(详细看3b1b的视频)

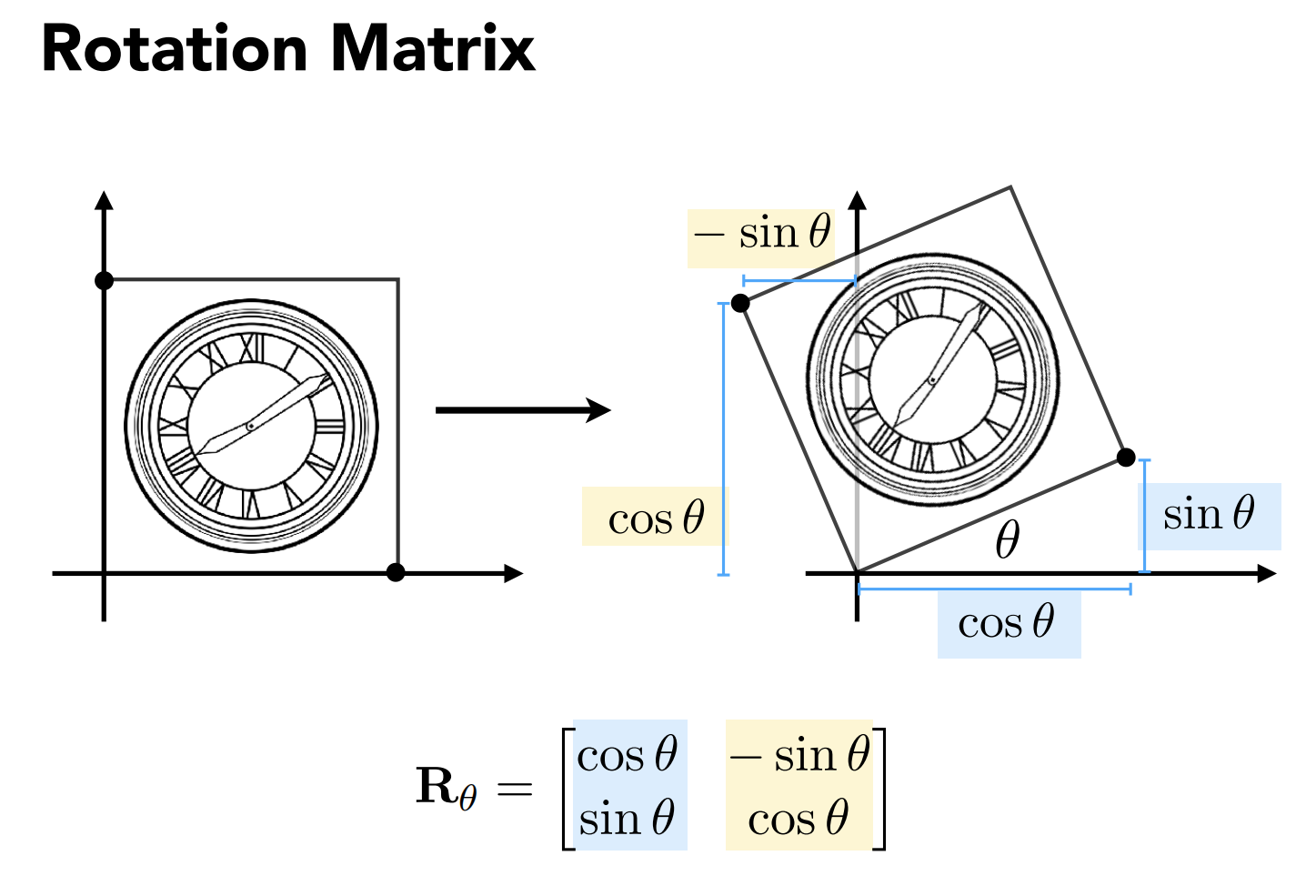
二维旋转矩阵

根据上面的知识，可以写出二维下的旋转矩阵：

齐次坐标系(Homogeneous coordinates)

如何表示平移变换？

对于二维平面上的变换，二维矩阵和二维坐标仅能表示线性变换，而线性变换不包括平移。

如果要表示平移，必须携程下面这种形式：

\begin{bmatrix} x_{out} \\ y_{out} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x_{in} \\ y_{in} \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}

可以看到，这种形式无论如何都无法表示成一个矩阵(不是齐次方程)。我们不希望平移变换是变换中的特例，为了用一个矩阵同时表示线性变换和平移变换，引入齐次坐标系的概念：

齐次坐标系中多引入了一个维度 \omega ,当它为0时表示向量，为1时表示点。于是二维平移变换就可以用上面的三维矩阵表示。

\omega 的取值为什么是1和0？这是因为这样取值不仅能使平移变换能用上面的矩阵表示，还有以下良好性质：

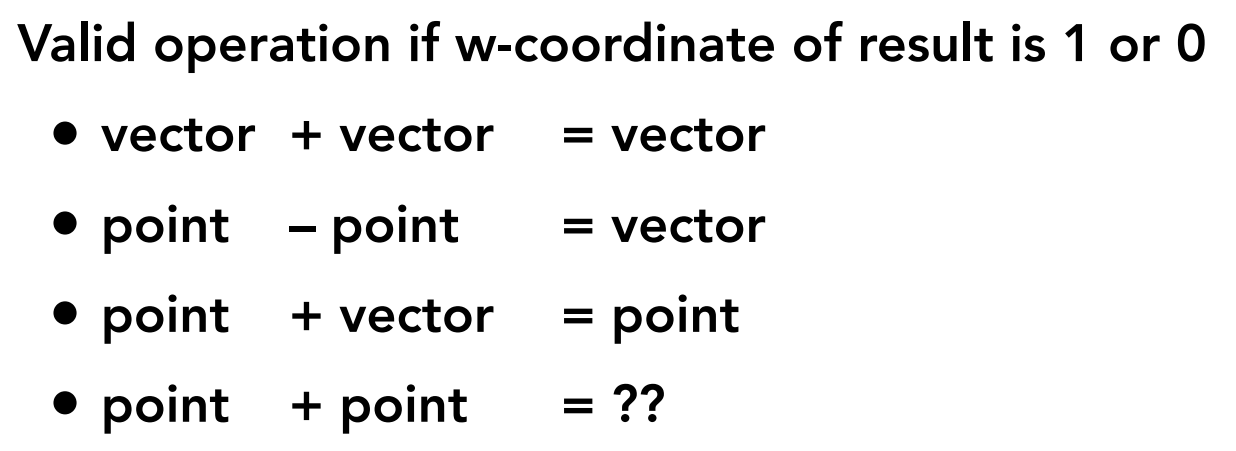
点+点本来就没意义；其他都完美符合点和向量的运算定义，实在是太优雅了！\omega 的取值不是0或1时，它的定义是：

这个定义在后面推导投影变换时会很有用。

将线性变换和平移结合？仿射变换！

如果想用一个矩阵表示 \begin{bmatrix} x_{out} \\ y_{out} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x_{in} \\ y_{in} \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix} ，可以写成以下形式：

\begin{pmatrix} x_{out} \\ y_{out} \\ 1 \end{pmatrix} = \begin{pmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_{in} \\ y_{in} \\ 1 \end{pmatrix}

简单计算一下就知道结果是正确的，齐次坐标的优雅再次体现：一个矩阵就能表示任何线性变换和平移的组合

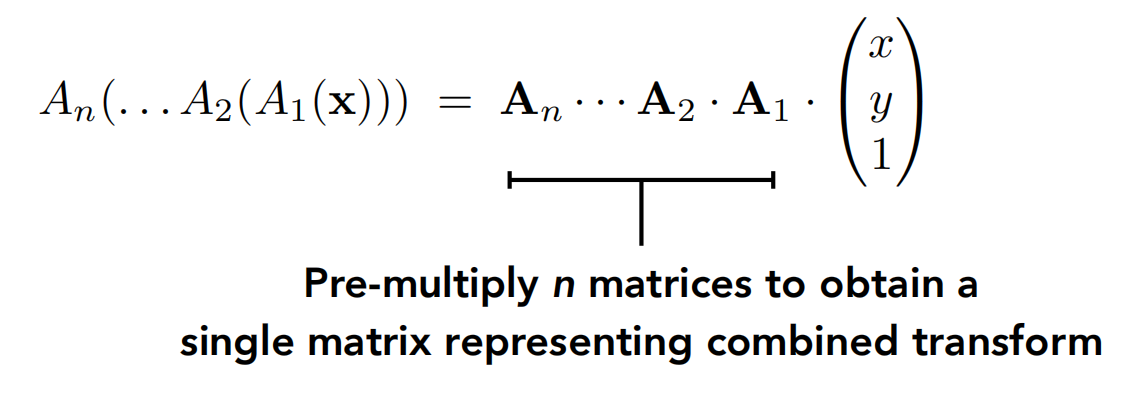
这就是仿射变换！这里需要明确注意，对于一个仿射变换矩阵，虽然它可能由无数多个矩阵组合而来，但最终它本质上表示的是先线性变换再平移变换。

如果想做先平移再线性，那就只能先写成类似于 \begin{pmatrix} x_{out} \\ y_{out} \\ 1 \end{pmatrix} = \begin{pmatrix} a & b & 0 \\ c & d & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_{in} \\ y_{in} \\ 1 \end{pmatrix} 的形式。

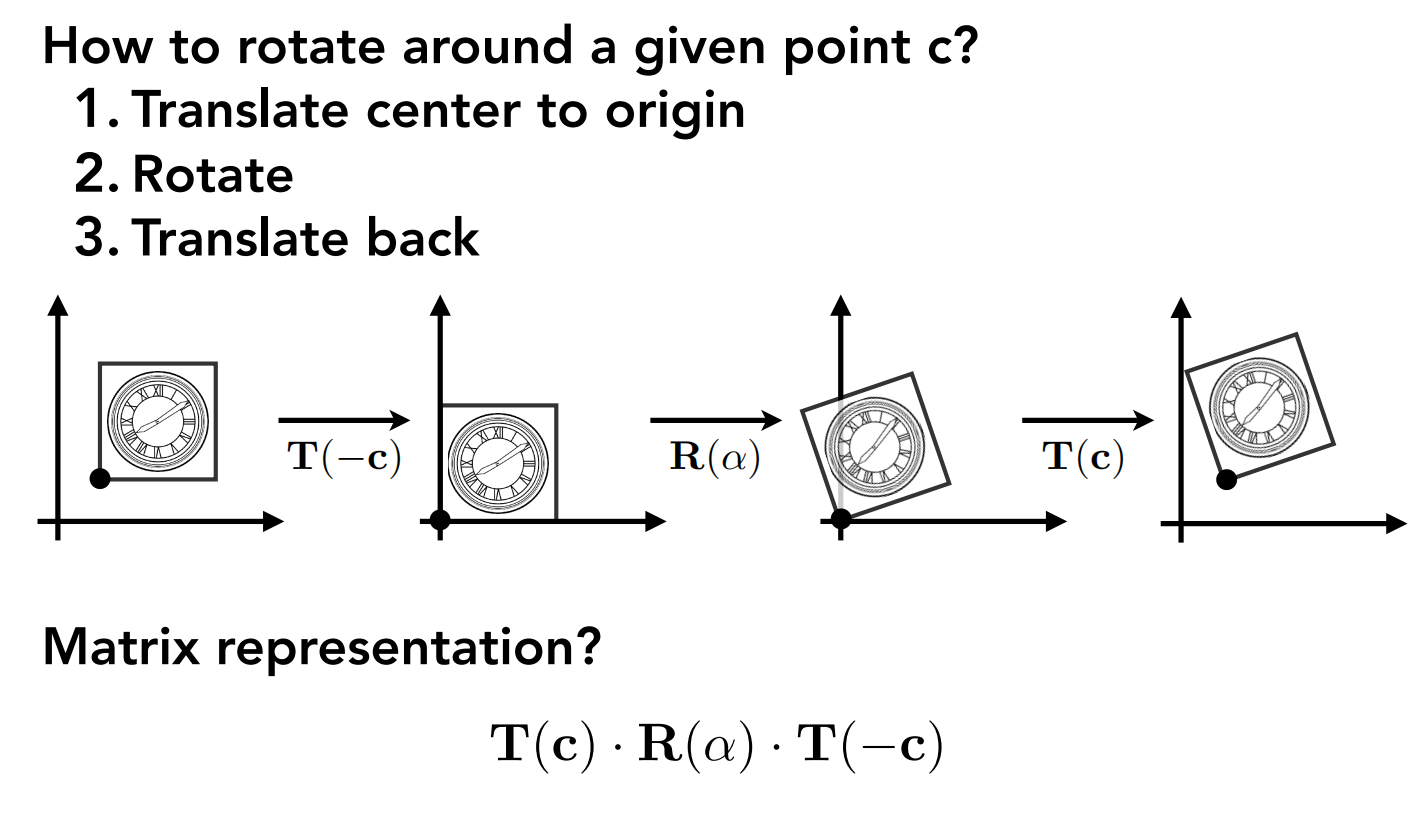
如何实现绕任意点的旋转？

绕任意点的旋转很难预判坐标轴的变换情况，想一次写出变换矩阵有点困难，可以通过如下步骤实现：

  • 先进行平移，将旋转点平移至原点

  • 通过旋转矩阵绕原点旋转对应角度

  • 再将旋转点平移到原来的位置