基础版:77. 组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[ [2,4] , [3,4] , [2,3] , [1,2] , [1,3] , [1,4] ]示例 2:
输入:n = 1, k = 1
输出:[[1]]
回溯整体思路和框架
vector<type> ans;
vector<vector<type>> result;
void dfs(起点) {
if (终止条件) {
存放结果;
return;
}
for (遍历本层所有元素(回溯树的一层)) {
处理节点;
dfs(新起点); // 递归
回溯,撤销处理结果
}
}回溯本质上就是DFS,是一种暴力搜索方式。回溯本身最核心的一步就是画出回溯树:
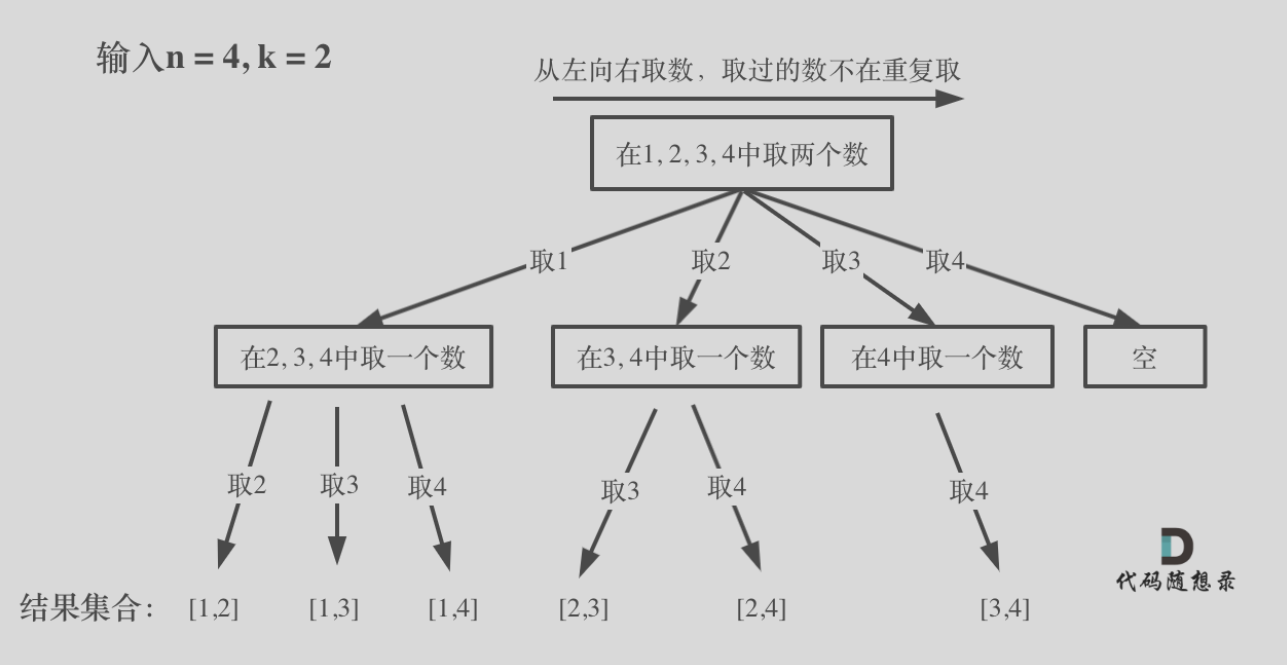
画出回溯树后,判断树层和树枝在特定题目和代码中的含义。
树层:每一层递归的后续选择列表。比如第一层中[1,2,3,4]处于同一层;处理1后,下一层递归中[2,3,4]处于同一层。树层的遍历在代码中体现为for循环调用dfs()
树枝:一条完整的树枝在组合问题中对应一个唯一的结果。抽象来说,一层的一次dfs()调用可以对应多条树枝。这个概念在后续回溯去重中比较重要
dfs(起点)参数中的"起点"是本次递归的起始元素,这里可以借用递归时的思维:dfs(起点)的作用是搜索完全部以"起点"开始处理的结果。比如对于本题,dfs(0)的作用是搜索下标为0及其之后所有元素的相关结果。
那为什么有些"起点"会被多次调用?比如dfs(1)不仅在第一层的第二次循环中被调用,在dfs(0) (第二层)的第一次循环中也会被调用,这样不会重复吗?
这是因为虽然同样都是dfs(1) ,但它们有个全局参数ans发生了改变。它们实际上是dfs(1,ans) ,而ans 不同。含义概述为:搜索以1 为起点,上层选择为ans 情况下的所有结果。
上面的分析不仅对于理解基本回溯很重要,同时对后面的各种去重理解也很重要。

