插值(Interpolation)与重心坐标(Barycentric Coordinates)
在图形渲染管线中,我们通常只知道三角形三个顶点的属性(如坐标、颜色、法线、纹理坐标等)。 但是,光栅化后的三角形内部包含成千上万个像素。为了算出三角形内部任意一点的属性,我们需要一种平滑过渡的方法 。
答案就是利用重心坐标插值。
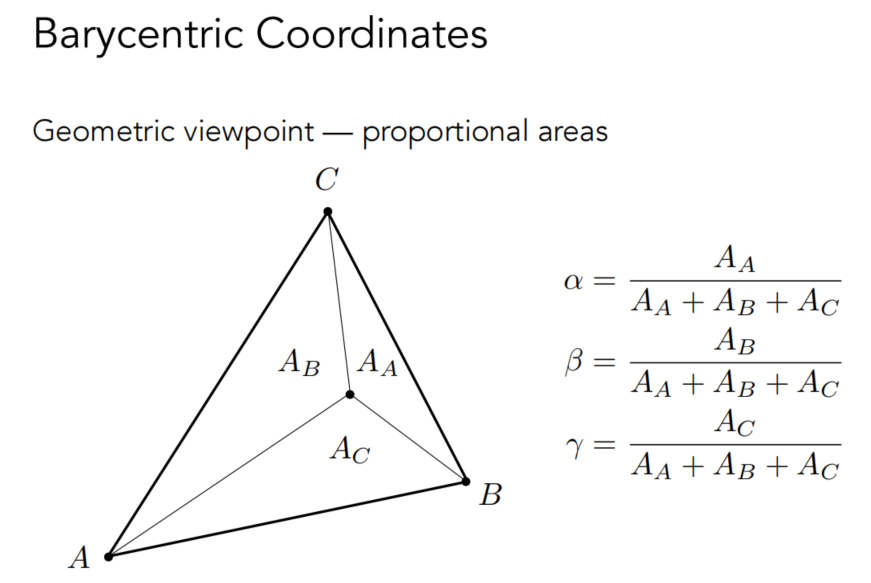
利用上图所示的面积比来定义重心坐标 (\alpha,\beta,\gamma) ,需要满足 \alpha+\beta+\gamma = 1 且均非负。
于是我们就可以用如下方式进行差值,其中V是插值后的属性,Vi是各顶点的属性:
上述公式成立的前提是属性V和重心坐标 (\alpha,\beta,\gamma) 是在同一个空间下算出来的,但实际渲染中往往没这么简单。
投影对重心坐标的影响(透视矫正)
三角形在透视投影中会发生形变,从而导致同样的点在投影后的重心坐标也跟着发生变化。因此在screen space和clip space下同一个点算出来的重心坐标往往不一样。直观一点的理解是:透视投影会产生近大远小的非线性拉伸,屏幕上的几何中心并不是三维空间中三角形的几何中心。
实际实现中,我们只有到了光栅化时才会有像素的概念。所以到了这一步才会计算重心坐标,即来自screen space。而模型中顶点上定义的各个属性显然是属于clip space的。要解决这个问题,我们就必须统一属性和重心坐标的空间。
重心坐标几乎只会在光栅化阶段计算,所以只能考虑将属性变换到screen space计算插值,再还原到clip space。通过相对比较复杂的数学证明,我们有下面的公式来计算插值:
(注意,公式中的重心坐标来自2D的screen space,属性V和顶点深度Z_i都来自clip space)
光栅化时,计算每个像素的深度公式如下:
计算每个像素的属性公式如下:
实际上可以说, \frac{1}{Z} 在screen space是线性的。
光栅化阶段,rasterizer接收到的是三个clip space坐标,并给出这个三角形的光栅化结果。rasterizer需要先进行透视除法,再进行viewport变换,再进行光栅化。
正常来讲,到这一步就已经丢失 Z_{clip} 和 W_{clip} 了,但是插值需要用到这两个属性,于是我们可以在透视除法时只除xyz,不除w,以四维向量的形式保存带深度的平面坐标,这样我们就留下了 W_{clip} ,而此时的 W_{clip} 就等于 -Z_{view} (要注意 Z_{view} \neq Z_{clip})。于是,我们可以直接用 W_{clip} 代替 Z_{view} 进行插值!代码如下:
//这里通过screen space的中心点坐标(x,y)计算重心坐标。
auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
// 下面的v[i]是三角形第i个顶点的,screen space坐标。它的z是映射后的深度,w直接没参与透视除法,仍然等于-z_view!
// Z是对真实的Z的插值,而zp是对映射后的[0.1,50]深度的插值
// 此处Z不用加负号。虽然w=-z,导致Z并不是对view space的z的插值结果
// 但是后面的插值都是除的w(应该要除z的),所以这个符号倒了两次,还是对的
float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
// z_buffer插值
float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
zp *= Z;
// color插值
Vector3f interpolated_color = alpha * t.color[0] / v[0].w() + beta * t.color[1] / v[1].w() + gamma * t.color[2] / v[2].w();
interpolated_color *= Z;由于view space到clip space仍然是线性的(不线性的变换是透视除法!),我们用view space的Z还是clip space的Z进行上述插值都是一样的。
任何属性的重心坐标插值都是上面的这套逻辑
纹理映射(Textrue Mapping)
纹理映射实际上是告诉shader不同的位置的kd应该取多少,通过改变漫反射来改变颜色,从而实现texture。(这个映射还可以用来改变该点别的信息,但无论如何都是为了表现texture)
每个三角形顶点都对应一对texture的uv坐标,三角形内部通过插值得到每个像素的uv坐标,从而进行像素级的纹理映射。下图展示了空间中的点如何映射到材质坐标上。不同点映射到同一个uv就实现了材质贴图的重复。

